THERMODYNAMIQUE - Processus irréversibles non linéaires

THERMODYNAMIQUE - Processus irréversibles non linéaires

Les progrès réalisés dans le domaine non linéaire sont beaucoup plus récents. On connaît cependant à leur sujet un critère d’évolution général régissant le comportement d’un système dissipatif, soumis à des contraintes stationnaires (Paul Glansdorff et Ilya Prigogine, 1954).

1. Critères d’évolution et de stabilité

Après décomposition de la production d’entropie d P en deux termes, sous la forme:

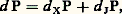avec:

on établit que le terme d ^XP possède un signe défini, soit d ^XP 諒 0, le signe d’égalité se rapportant à l’état stationnaire. Ce critère exprime d’ailleurs une généralisation du théorème du minimum de production d’entropie puisque, dans le domaine linéaire décrit ci-dessus, on a pour les mêmes contraintes stationnaires: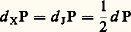

avec des coefficients phénoménologiques L^ij constants. Bien que non variationnel, car d ^XP n’est généralement pas réductible à la différentielle exacte d’un potentiel, ce critère présente de l’intérêt pour l’étude de la stabilité des états, stationnaires ou non, éloignés de l’équilibre. Le degré de généralité de ce nouveau critère n’est guère limité que par l’hypothèse préalable de l’équilibre local défini par la relation (13) de l’article relatif aux lois fondamentales et de la stabilité de cet équilibre (loi de Gibbs, condition C^V 礪 0, etc.). On montre que la différentielle seconde 嗀²S de l’entropie devient une forme quadratique définie négative (en variables énergie, volume, titres). On peut, dès lors, adopter cette expression comme fonction de Liapounoff et en déduire un critère de stabilité par rapport aux petites perturbations sous la forme:

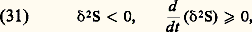autour du processus irréversible considéré et soumis à des contraintes fixes. La dernière inégalité exprime la stabilité, car elle implique à tout instant la régression des fluctuations qui ont engendré l’écart 嗀²S.

Ce dernier critère ainsi que le critère d’évolution d ^XP 諒 0 conduisent tous deux à la forme explicite de la condition de stabilité. Celle-ci s’exprime en termes de fluctuations des courants et des forces généralisées sous la forme:

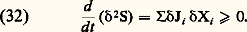On observe immédiatement qu’autour d’un état d’équilibre la stabilité est identiquement assurée en vertu du second principe (11) puisque, dans ce cas, on a:

Il en est de même dans tout le domaine de la thermodynamique linéaire, car, d’après les égalités (24), le signe du membre de droite de la relation (32) reste nécessairement identique à celui de la production d’entropie P donnée en (15). Toutefois, il n’en est plus ainsi à grande distance de l’équilibre, où la condition de signe dans (32) peut être mise en défaut. Cette éventualité se présente en général pour des contraintes élevées et lorsque le système est le siège soit d’effets d’autocatalyse, soit de phénomènes convectifs (origine de la turbulence). Dans chacun de ces deux cas, le système peut évoluer, à la suite d’une fluctuation, vers un régime totalement différent, stationnaire ou périodique – l’essentiel étant que ce nouveau régime peut présenter une structure entièrement imprévue.

En accroissant progressivement les contraintes, on constate qu’un tel changement se présente pour une valeur critique au-delà de laquelle la nouvelle solution stable chasse l’ancienne devenue instable. C’est l’état marginal . Ici, les lois de la thermodynamique entraînent des conséquences quelque peu inattendues puisque, à l’inverse de la dégradation classique par dissipation, le régime qui s’établit peut être plus structuré que le précédent. Cet accroissement de structure est tantôt spatial et donne lieu à une structure dissipative , tantôt temporel sous la forme de cycles limites . Un grand nombre de possibilités existe. Le mouvement cellulaire de Bénard , prenant naissance au sein d’une couche horizontale de fluide chauffée par le bas, constitue l’un des premiers et des plus édifiants exemples de telles structures. L’expérience et le calcul montrent que certaines réactions chimiques provoquent des effets du même type (cf. photo). À l’heure actuelle, le principal intérêt de la thermodynamique des phénomènes irréversibles se rapporte au lien avec les processus biologiques (cf. ORDRE ET DÉSORDRE EN BIOLOGIE, chap. 4 dans le Symposium ).

2. Thermodynamique et dynamique

Dès son origine, le second principe a joué un rôle essentiel dans l’interprétation philosophique des concepts fondamentaux de la science. Henri Bergson considérait ce principe comme la plus «métaphysique» des lois de la nature, et A. Eddington associait l’entropie à la flèche du temps.

Une question fondamentale consiste à réconcilier le concept d’irréversibilité exprimé par le second principe avec les lois de la dynamique (classique ou quantique). Les travaux fondamentaux de L. Boltzmann, cités plus haut, apportent à ce problème une contribution importante qui demeure pourtant incomplète. Ce physicien a clairement reconnu que le second principe ne s’applique qu’à des systèmes macroscopiques formés d’un nombre immense de particules, de l’ordre du nombre d’Avogadro (6,02 憐 10²³). D’où l’adoption d’une description statistique du système et, dans cette perspective, Boltzmann établit l’équation cinétique d’un gaz dilué régissant le comportement de la fonction f de distribution des vitesses (cf. théorie CINÉTIQUE DES FLUIDES). Il en déduit ensuite une fonctionnelle H de f qui ne peut que décroître au cours du temps, conformément au théorème H , bien connu sous ce nom ^{[cf. BOLTZMANN (L.)]}. Cette grandeur fournit le premier modèle microscopique de l’entropie.

La théorie de Boltzmann, quoique très convaincante du point de vue physique pour les gaz dilués, ne peut cependant pas être considérée comme d’une portée générale, résolvant le problème des relations fondamentales entre dynamique et thermodynamique. Ce problème reste encore à présent d’un intérêt considérable. Il est clair tout d’abord qu’il ne suffit pas qu’un système soit composé d’un grand nombre de particules pour le voir tendre vers l’équilibre thermodynamique. Ainsi, dans un ensemble de molécules indépendantes et sans interaction, aucun équilibre thermique ne pourrait s’établir et l’évolution de cet ensemble ne tendrait nullement vers l’état correspondant au maximum de son entropie. La théorie ergodique , telle qu’elle est exposée dans l’ouvrage de A. I. Khinchin (1949), fixe d’ailleurs les conditions pour que l’approche de l’équilibre devienne possible. Toutefois, les précisions qu’apporte cet auteur sont plutôt relatives aux conditions permettant une description en termes de thermodynamique d’équilibre qu’aux propriétés régissant l’évolution du système vers cet état d’équilibre. Sous ce rapport, le développement de la mécanique statistique des états de non-équilibre a entraîné de nouveaux progrès. En effet, elle permet d’établir sous quelles conditions on peut associer à l’évolution d’un grand système une fonction à variation monotone. Une telle fonction devient alors un modèle microscopique de l’entropie. Cette possibilité existe notamment pour les grands systèmes dont les molécules sont en interaction sous l’effet de forces à courte portée , telles que, par exemple, les forces de Van der Waals. En revanche, la construction d’un modèle microscopique de l’entropie est beaucoup plus compliquée lorsque les interactions correspondent à des forces à longue portée telles que les forces gravifiques. Il faut donc être très prudent dès qu’on envisage une extrapolation du second principe à l’échelle cosmologique comme l’avait fait Clausius par la citation rapportée au début de cet article.

Ces considérations ont montré que les lois de la dynamique, lorsqu’elles sont appliquées à la limite de grands systèmes, présentent parfois des caractéristiques entièrement nouvelles. En particulier, la propriété d’invariance des lois de la dynamique par rapport au renversement du temps disparaît à cette limite (I. Prigogine, 1972). Une telle situation se présente aussi avec la notion de transition de phase qui, semblablement, n’acquiert un sens précis qu’à la limite d’un grand système. Cette rupture de symétrie introduit la notion d’irréversibilité et conduit à la description phénoménologique de la thermodynamique. D’autres caractères remarquables de phénomènes évolutifs peuvent apparaître dans le cadre de cette description macroscopique. Il en est de même, notamment, à grande distance de l’équilibre thermodynamique pour les structures dissipatives signalées plus haut. Certaines d’entre elles peuvent correspondre à des ruptures de symétrie qui rendent le système inhomogène. Dès lors, les régions qui diffèrent par leur composition deviennent, en général, le siège d’évolutions distinctes. On voit apparaître ainsi progressivement dans le cadre de la description thermodynamique une dimension historique du temps , imposée par l’ordre de succession des structures. Son interprétation dépasse celle qui relève du simple problème de l’irréversibilité.

En résumé, la conception du temps à laquelle conduisait la mécanique classique ou quantique provenait de l’extrapolation de résultats obtenus à partir de son application à des petits systèmes . Au contraire, la thermodynamique est consacrée à l’étude des grands systèmes , et la notion de temps y apparaît avec des caractéristiques nouvelles et originales. Cette constation met en évidence tout l’intérêt de la thermodynamique dans l’épistémologie des sciences.

3. Thermodynamique et biologie

Dans son livre intitulé L’Ordre biologique , A. Lwoff écrit: «Un certain aspect de l’ordre est l’arrangement déterminé présent dans la constitution existante des choses. L’ordre peut être considéré aussi comme une séquence, ou une succession, dans l’espace ou dans le temps. L’ordre biologique est tout cela, et plus spécialement une séquence dans l’espace et dans le temps.» On peut se demander comment cet ordre ainsi défini se situe par rapport aux grandes lois d’organisation de la physique et, en particulier, de la thermodynamique.

Celle-ci prévoit qu’un système isolé évolue dans le temps vers le désordre. En revanche, en biologie et en sociologie, l’idée d’évolution est associée à une croissance de l’organisation et à la formation de structures de plus en plus complexes. En conséquence, on a longtemps pensé que l’organisation biologique ne pouvait être décrite à partir des lois de la physique. Actuellement, nombre de biologistes considèrent qu’il suffit d’appliquer la thermodynamique à l’ensemble «être vivant plus environnement» pour lever cette difficulté. Cependant, cette interprétation est largement insuffisante. Elle introduit différemment la notion de « système ouvert » mais n’apporte rien de plus à celle de «l’être vivant». Elle n’explique pas en particulier comment interviennent d’une part, le hasard et d’autre part, les lois déterministes dans la formation des structures biologiques. L’analyse du rôle de la non-linéarité en thermodynamique, exposée plus haut, et qui a conduit au concept de structure dissipative a permis de répondre à ces questions.

Ordre biologique et structures dissipatives

Les systèmes biologiques sont des systèmes ouverts échangeant de la matière et de l’énergie avec le monde extérieur. Ils se caractérisent par un ordre spatial et temporel tout comme celui des structures dissipatives définies plus haut. Il convient donc d’examiner dans quelle mesure celles-ci interviennent dans l’établissement de l’ordre biologique.

La question est relativement plus simple à traiter pour l’organisation temporelle, car l’évolution du système est alors régie par un nombre réduit d’équations différentielles ordinaires tandis que l’étude des structures spatiales ou spatio-temporelles requiert l’analyse plus complexe d’équations aux dérivées partielles.

Au point de vue temporel, les phénomènes d’auto-organisation les plus communs sont, soit l’apparition d’états stationnaires multiples, soit l’évolution vers un régime d’oscillations entretenues correspondant à un cycle limite autour d’un état stationnaire devenu instable à la suite d’une bifurcation. Les exemples biologiques de tels phénomènes sont nombreux, et certains sont brièvement détaillés ci-dessous.

S’il est vrai que les phénomènes périodiques sont connus en chimie non biologique, comme l’indique la réaction de Belousov-Zhabotinsky (cf. photo) il faut reconnaître qu’ils sont encore plus abondants en biologie. Ils interviennent à tous les niveaux de l’organisation biologique, avec des périodes allant de la seconde (système nerveux) à l’année (systèmes écologiques). Le fonctionnement périodique de certaines cellules nerveuses, lié à leur propriété d’excitabilité, est connu depuis longtemps. Le rythme cardiaque et le rythme respiratoire sont tous deux contrôlés par le système nerveux. Des oscillations d’une période de quelques minutes sont connues dans le métabolisme cellulaire. Elles sont dues à la régulation de l’activité de certaines enzymes. D’autres oscillations, d’une période de l’ordre de l’heure, affectent la synthèse de certaines protéines et résultent de la régulation génétique. Les rythmes circadiens, d’une période proche de 24 heures, sont omniprésents. Toutefois, leur mécanisme reste encore obscur. De périodes plus longues, de l’ordre de quelques jours ou du mois, sont les cycles hormonaux contrôlant la reproduction chez les mammifères. Enfin, à une autre échelle pouvant atteindre quelques années, on connaît depuis longtemps les variations périodiques de populations animales résultant notamment des interactions entre un prédateur et sa proie.

Tous ces phénomènes rythmiques peuvent être interprétés comme l’apparition d’un ordre temporel, sous forme d’oscillations entretenues du type cycle limite, au-delà d’une instabilité de non-équilibre dans un système ouvert régi par des équations cinétiques non linéaires. Cette situation correspond fidèlement à la définition des structures dissipatives en thermodynamique. Les variables dont l’évolution est décrite par ces équations sont, selon le cas, des concentrations d’ions, de métabolites, d’enzymes ou d’hormones, voire des populations de prédateurs ou de proies. Il est remarquable que quelle que soit la nature des éléments du système considéré les interactions non linéaires entre les éléments donnent lieu à des phénomènes identiques régis par des équations différentielles assez semblables.

La raison pour laquelle les phénomènes périodiques sont aussi fréquents en biologie tient à la non-linéarité des processus de régulation, sous forme de rétroactions positives ou négatives, qui s’exercent à tous les niveaux de l’organisation biologique. À cet égard, les oscillations métaboliques sont probablement celles dont le mécanisme est le mieux connu au niveau moléculaire. Elles présentent ainsi un double intérêt, pour leur rôle dans la dynamique cellulaire et pour leur fonction de modèle de rythme biologique. Les prototypes en sont les oscillations glycolytiques dans la levure et dans le muscle, et les oscillations des adénosines monophosphates (AMP) cycliques dans les amibes Dictyostelium discoideum .

Nous examinerons successivement le mécanisme de ces deux phénomènes oscillants, de même qu’un exemple de transition entre états stationnaires multiples impliquant un processus de régulation génétique.

Cycle de la glycolyse

Ce cycle est l’une des voies importantes de production d’énergie cellulaire, sous forme d’adénosine triphosphate (ATP), à partir de glucose. On a observé que, dans des cellules de levures et dans les muscles, la concentration des intermédiaires glycolytiques peut présenter des oscillations entretenues dont la période est de quelques minutes (cf. RYTHMES BIOLOGIQUES, fig. 2). Parmi les différentes enzymes du cycle de la glycolyse, la phosphofructokinase semble jouer le rôle principal dans l’apparition de ce phénomène périodique. Cette enzyme est allostérique, en ce sens qu’elle est formée d’unités équivalentes possédant des sites réactionnels spécifiques pour la fixation du substrat (fructose-6-phosphate) et du produit de réaction sous forme d’adénosine diphosphate (ADP). Chaque unité existe sous deux états conformationnels T et R, le second ayant une plus grande activité catalytique et/ou une plus grande affinité pour le substrat. L’équilibre conformationnel est «concerté», autrement dit, si l’une des unités formant la molécule change de conformation, les autres unités font de même. La particularité de la phosphofructokinase tient à ce que sa régulation est autocatalytique: en effet, les produits de la réaction (ADP, fructose diphosphate) déplacent l’équilibre conformationnel en faveur de la forme active de l’enzyme. C’est la combinaison de ces deux effets qui est à l’origine des oscillations (fig. 1).

La réaction de la phosphofructokinase gouverne les oscillations de la chaîne glycolytique tout entière. C’est ainsi que l’on peut réduire l’étude du comportement dynamique du cycle de la glycolyse à celle de la réaction de la seule phosphofructokinase, c’est-à-dire à deux équations différentielles non linéaires pour les concentrations des variables S et P, ce qui rend possible la représentation de la fig. 1. Lorsque l’on traite la cinétique de l’enzyme dans le cadre du modèle allostérique «concerté» de Monod-Wyman-Changeux, en tenant compte de la rétroaction positive exercée par le produit de réaction, on obtient les équations: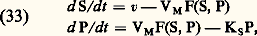

où v et V^M dénotent, respectivement, la vitesse d’injection de substrat et la vitesse maximum de la réaction enzymatique, tandis que la constante K^S se rapporte à la vitesse d’élimination du produit. La fonction F(S, P) contient toute la non-linéarité due à la cinétique coopérative de la phosphofructokinase et au caractère autocatalytique de la réaction. Cette fonction, qui n’est autre que la vitesse de réaction, est de la forme:

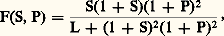dans le cas le plus simple où l’on suppose que l’enzyme est formée de deux sous-unités, et que la forme T est inactive.

Le comportement résultant des équations cinétiques de ce schéma est étudié en partant des différentes données expérimentales disponibles. On détermine d’abord l’état stationnaire de non-équilibre admis par les équations (33). Cet état est obtenu en imposant une valeur constante au substrat et au produit, soit: (d S/dt ) = (d P/dt ) = 0. On étudie ensuite la réponse du système à de petites perturbations autour de cet état. Dans certaines conditions, précisées par cette analyse, les perturbations peuvent s’amplifier au cours du temps. L’état stationnaire est alors instable et le système évolue vers un régime d’oscillations entretenues des concentrations S et P au cours du temps. Ces oscillations correspondent à une variation périodique de l’activité enzymatique (fig. 2). Dans l’espace des phases (S, P), le système tend vers un cycle limite entourant l’état stationnaire instable. Ainsi, quelles que soient les valeurs initiales de S et P, le système évolue toujours vers le même régime oscillant dont l’amplitude et la période sont fixées par les conditions expérimentales et les valeurs des paramètres. Ces caractéristiques de stabilité de la période et de l’amplitude sont celles de la plupart des rythmes biologiques.

L’analyse détaillée du comportement oscillant du modèle se fait au moyen de simulations numériques sur calculateur électronique. On peut ainsi déterminer l’effet d’une variation de la vitesse d’injection de substrat (paramètre v dans les équations (33)). L’analyse du modèle montre qu’en dessous d’une vitesse critique v¹, le système évolue vers un état stationnaire stable. Quand on augmente progressivement la vitesse, des oscillations du type cycle limite apparaissent quand v dépasse v¹, mais les oscillations disparaissent dès qu’une seconde vitesse critique est atteinte: le système évolue alors vers un nouvel état stationnaire stable. Ce comportement est en accord avec les observations expérimentales. Un accord qualitatif et quantitatif est également obtenu pour d’autres effets dépendant d’autres paramètres, de même que pour le déphasage induit par addition d’ADP au cours des oscillations. Les oscillations glycolytiques représentent donc une structure dissipative temporelle dont l’origine est comprise en détail depuis son niveau moléculaire. Ce résultat est important, car il s’agit de réactions essentielles pour l’énergétique des cellules vivantes.

L’agrégation des acrasiales

L’agrégation des acrasiales fournit un autre exemple particulièrement approprié de structures dissipatives en biologie, car ce phénomène met en jeu au moins deux bifurcations distinctes. Les acrasiales appartiennent à une classe d’amibes dont l’espèce la plus étudiée est Dictyostelium discoideum . Ces amibes sont dites sociales parce qu’elles correspondent à une population d’individus se présentant sous les formes unicellulaire et multicellulaire à deux stades successifs de leur cycle de vie.

Au sortir de spores, les amibes croissent et se reproduisent à l’état unicellulaire. Cette situation se prolonge jusqu’à ce que la nourriture, fournie principalement par des bactéries, vienne à manquer. À ce moment, les amibes cessent de se reproduire et entrent dans une période d’interphase qui dure quelque huit heures. Vers la fin de l’interphase, les amibes commencent à s’agréger autour de certaines d’entre elles fonctionnant comme centres d’agrégation. L’agrégation se fait en réponse à des signaux chimiotactiques émis par les centres. L’agrégat ainsi formé migre jusqu’à ce que les cellules se différencient pour former une tige surmontée d’un sac contenant les spores.

L’existence d’un mécanisme de communication intercellulaire pendant l’agrégation, jointe au fait que les amibes se différencient en deux types de cellules seulement, font que les acrasiales constituent un modèle de choix dans l’étude de la biologie du développement.

Dans Dictyostelium discoideum , l’agrégation se fait de manière périodique. Les films de l’agrégation montrent l’existence d’ondes concentriques d’amibes se dirigeant vers le centre avec une périodicité de quelques minutes.

La nature du facteur chimiotactique est connue: il s’agit de l’adénosine monophosphate cyclique (cAMP), substance impliquée dans de nombreux autres processus biochimiques comme les régulations hormonales. Les centres d’agrégation émettent de façon autonome et périodique les signaux de cAMP. Les autres cellules répondent en se dirigeant vers les centres et en relayant les signaux vers la périphérie du territoire d’agrégation. L’existence d’un mécanisme de relais du signal chimiotactique permet à chaque centre de contrôler l’agrégation de quelque cent mille amibes.

L’analyse du processus d’agrégation met en évidence l’existence de deux types de bifurcations. Tout d’abord, l’agrégation même représente une structuration dans l’espace. Au départ, les amibes sont réparties de façon homogène. Lorsque certaines d’entre elles commencent à sécréter le signal chimiotactique, il se crée des fluctuations locales dans la concentration de cAMP. L’analyse d’un modèle montre que pour une valeur critique des paramètres du système (coefficient de diffusion de l’AMP cyclique, motilité des amibes, etc.), les fluctuations s’amplifient: la répartition homogène est devenue instable et les amibes évoluent vers une répartition spatiale hétérogène. Cette nouvelle répartition s’accompagne donc d’une rupture de symétrie de la distribution initiale, et correspond à l’accumulation des amibes autour de centres d’agrégation. Du point de vue de la thermodynamique, ce comportement correspond fidèlement à celui d’une structure dissipative.

Cette analyse ne rend pas compte du caractère périodique de l’agrégation observée chez certaines espèces d’acrasiales telles Dictyostelium discoideum . Pour comprendre l’origine de la périodicité, il est nécessaire d’étudier plus en détail le mécanisme de synthèse du signal chimiotactique. Sur une base d’observations expérimentales, on peut décrire ce mécanisme par le schéma de la figure 3. Sur la surface des cellules se trouvent des récepteurs liant les molécules de cAMP. Ce récepteur fait face au milieu extracellulaire et est lié de façon fonctionnelle à l’enzyme assurant la transformation intracellulaire de l’ATP en cAMP, dénommée adénylate cyclase. Le cAMP ainsi synthétisé est transporté au travers de la membrane dans le milieu extracellulaire où il est dégradé par une enzyme sécrétée par les amibes: la phosphodiestérase. L’expérience montre que la liaison du cAMP extracellulaire au récepteur membranaire provoque l’activation de l’adénylate cyclase.

Sur la base de cette rétroaction positive, l’analyse d’un modèle pour l’évolution temporelle des trois variables ATP, cAMP intracellulaire et cAMP extracellulaire a permis d’unifier différents types de comportements observés au cours de l’agrégation. Deux des paramètres clés du modèle sont les activités de l’adénylate cyclase (s ) et de la phosphodiestérase (k ). Pour un ensemble de valeurs de s et k , le système admet un état stationnaire unique et instable. Chaque fois que les valeurs de ces deux paramètres correspondent à un point de ce domaine, l’instabilité du système provoque son évolution vers un régime d’oscillations entretenues. Ce régime correspond à la synthèse périodique de signaux de cAMP et peut être associé au fonctionnement des centres d’agrégation. Dans une région de l’espace des paramètres contiguë à la précédente, l’état stationnaire est stable mais excitable: le système est capable d’amplifier de manière pulsative de petites perturbations dans la concentration extracellulaire de cAMP. Cette propriété peut être identifiée à la capacité qu’ont les cellules de relayer les signaux de cAMP émis par les centres d’agrégation. Enfin, dans la zone extérieure aux domaines précités, le système évolue vers un état stationnaire stable et non excitable.

Des études sur le développement du mécanisme de communication par signaux de cAMP au cours de l’interphase montrent que les cellules sont tout d’abord incapables de répondre à des signaux de cAMP extracellulaire. Ensuite, progressivement elles relaient ces signaux appliqués de l’extérieur avant de pouvoir les synthétiser périodiquement de façon autonome. Toutes les amibes sont en fait capables de ce dernier type de réponse, bien que quelques-unes seulement deviennent des centres au cours de l’agrégation. La discussion qui précède suggère un chemin de développement du mécanisme de communication dans l’espace des paramètres s et k , pour expliquer la séquence des transitions successives: absence de relais – relais – oscillations, observée expérimentalement. Les centres d’agrégation seraient ainsi les cellules pour lesquelles le couple de valeurs des paramètres s et k aurait atteint le plus rapidement un point dans le domaine instable au cours de l’interphase. Le contenu de ces cellules en adénylate cyclase et en phosphodiestérase serait tel que la synthèse de cAMP ne pourrait procéder que de façon périodique.

Multiplicité d’états stationnaires en régulation génétique

La figure 4 représente le schéma proposé par J. Monod et F. Jacob pour la régulation de la synthèse des protéines dans un système comportant deux chemins enzymatiques distincts. Le gène régulateur RG de chaque enzyme produit un répresseur non actif R qui, en se combinant avec le produit P du chemin enzymatique opposé, forme le répresseur Re; ce dernier bloque la formation de l’enzyme E à partir du gène de structure G, par l’intermédiaire de l’ARN messager. À ce schéma il faut ajouter le fait important que le produit P, résultant de l’action de l’enzyme sur le substrat, n’a pas seulement un rôle régulateur, mais qu’il intervient également dans des réactions métaboliques schématisées par l’étape:

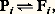avec i = 1, 2, et où Fⁱ est un produit résultant de la transformation de Pⁱ .

On écrit, pour l’ensemble formé par les deux chemins enzymatiques, des équations cinétiques régissant l’évolution dans le temps des concentrations des enzymes, des ARN messagers, des produits et des répresseurs, ainsi que des gènes, chacun dans leur état fermé (complexe par Re) ou ouvert. On a de plus la condition physique suivante: le gène est soit ouvert, soit fermé.

La vitesse du processus global est supposée déterminée par les vitesses de synthèse de l’ARN messager et de l’enzyme. Comme dans l’exemple précédent, les équations cinétiques sont traitées par ordinateur, mais cette fois pour un régime stationnaire. On commence par une valeur de ¹ correspondant à l’équilibre de la réaction métabolique. Les autres paramètres du système, tels que la valeur des différentes concentrations et constantes cinétiques, sont maintenus constants. Les équations cinétiques possèdent alors une solution unique. En faisant varier ¹, on s’écarte de l’équilibre et on atteint une valeur critique à partir de laquelle la solution thermodynamique devient instable, le système se plaçant alors sur une nouvelle branche de solutions stables des équations cinétiques. C’est une région à trois états stationnaires, mais le troisième état est instable.

On passe ainsi brusquement d’une branche à concentration faible en enzyme E¹ et forte en enzyme E² à une autre où la situation inverse prévaut. La conclusion importante est l’apparition d’une différentiation fonctionnelle profonde dans le système, sans qu’un changement soit intervenu dans l’information portée par le matériel génétique, et cela par suite de la non-linéarité de la cinétique et de son couplage avec l’environnement loin de l’équilibre thermodynamique. Pour certaines valeurs des paramètres, les trois états stationnaires disparaissent, la variation de la concentration de l’enzyme en fonction de ¹ étant donnée par une courbe sigmoïde.

Des transitions entre états stationnaires multiples ont été invoquées dans de nombreux autres processus cellulaires, tels le changement de perméabilité des membranes biologiques au cours de l’excitation nerveuse.

Morphogenèse

L’application du concept thermodynamique de structure dissipative en biologie, s’étend également au problème de la morphogenèse, c’est-à-dire à la formation de structures spatiales au cours du développement. Ce processus a lieu chez tous les organismes, des plus simples – comme les amibes acrasiales évoquées précédemment, où la structure résulte d’une différenciation en deux types de cellules et consiste en une tige surmontée de spores – jusqu’aux plus complexes, tels les embryons. La connaissance des mécanismes contrôlant la morphogenèse n’est pas encore suffisamment complète pour permettre l’élaboration de modèles appropriés à l’étude de la dynamique de ce phénomène. Toutefois, la théorie des structures dissipatives a été appliquée pour expliquer la formation de structures spatiales régulières au cours du développement. Une application spécifique concerne la formation séquentielle de compartiments dans les disques imaginaux de la drosophile; ces compartiments résulteraient d’une succession de bifurcations de structures spatiales à mesure que la taille des disques croît au cours du développement. À une échelle plus macroscopique encore, d’autres études suggèrent que la formation du nid et l’organisation des aires d’exploitation chez les insectes sociaux peuvent être interprétées en termes de structures dissipatives résultant des communications (interactions non linéaires) entre les insectes membres de la colonie.

Autres développements

L’analyse des processus d’auto-organisation temporelle a mis en lumière la possibilité d’oscillations non périodiques dans les systèmes physico-chimiques et biologiques. Ce type de comportement, bien que produit par des équations déterministes, possède un caractère aléatoire et, pour cette raison, est dénommé «chaos». L’apparition de ce phénomène dans les systèmes biologiques a été discutée en écologie, de même que pour un système biochimique à régulation multiple. L’analyse de ce dernier système a mis en lumière la possibilité d’un nouveau phénomène, à savoir la coexistence de deux régimes périodiques stables. Pour un même ensemble de conditions, un système biologique pourrait donc osciller avec des périodes et des amplitudes différentes selon les conditions initiales. Ce processus illustre une fois de plus la richesse de comportement des systèmes à cinétique non linéaire fonctionnant loin de l’équilibre thermodynamique.

Stade prébiotique

À côté du rôle joué par les structures dissipatives dans le fonctionnement actuel des êtres vivants, il convient d’évoquer la possibilité de leur participation à l’évolution prébiotique.

Le rôle possible des structures dissipatives dans la synthèse abiotique des polypeptides par condensation sur des surfaces catalytiques a été étudié par A. Katchalsky et ses collaborateurs. De son côté, en supposant l’existence d’un ensemble de macromolécules biologiques au stade prébiotique, M. Eigen a montré que le système évolue vers une self-organisation par suite d’une succession d’instabilités.

Il faut distinguer au moins deux types de problèmes: d’une part, la formation de polymères d’intérêt biologique remplissant des fonctions que les monomères ne peuvent accomplir (un exemple bien connu en est la synthèse de polymères qui jouent le rôle de matrice [template ] pour leur propre réplication ou pour leur synthèse d’autres macromolécules); d’autre part, en supposant que des populations de molécules d’intérêt biologique peuvent se répliquer, quelle sera l’évolution ultérieure d’un tel système?

Des modèles permettent de montrer que la synthèse par réplication, par exemple celle des acides nucléiques sur template , ne devient dominante par rapport au mécanisme ordinaire de propagation en chaîne qu’à partir d’une distance critique de l’équilibre et qu’elle correspond dès lors à une première instabilité.

M. Eigen considère le second point: les phénomènes de réplication conduisent à des erreurs (un type nouveau de fluctuations) qui peuvent être soit amorties, soit amplifiées (cf. GÉNÉTIQUE, MUTATIONS). L’évolution correspond à une suite de «catastrophes» d’instabilités. Les fluctuations sont amplifiées jusqu’à l’apparition éventuelle d’un état dominé par certains types de macromolécules et pourvu d’une stabilité suffisante par rapport aux fluctuations qu’il engendre lui-même.

Pendant longtemps, le développement scientifique s’est accommodé plus ou moins implicitement de cette opinion que les lois de la physique n’avaient aucun rapport avec celles de la biologie et qu’elles étaient même incompatibles. À présent, et depuis au moins une décennie, les progrès accomplis par la thermodynamique non linéaire des processus irréversibles dans ses rapports avec les propriétés des cinétiques chimiques ont complètement retourné cette opinion. Au point même, que pour les mieux avertis, et comme en témoignent les quelques applications évoquées succinctement ci-dessus, l’adaptation des lois de la physique à la biologie se présente comme faite en quelque sorte sur mesure dès qu’on pénètre davantage l’étude de leurs mécanismes.

4. Transitions de non-équilibre; bifurcations et fluctuations

Dans un grand nombre de situations d’intérêt physique, il arrive que l’évolution d’un système soit régie par des lois non linéaires . Nous allons illustrer cette éventualité par un exemple chimique qui fait intervenir le phénomène de la catalyse . Considérons la décomposition de l’éther par pyrolyse en phase gazeuse. Dans des conditions usuelles, ce processus est relativement lent. L’addition de quelques pour cent d’iode, catalyseur, suffit pour faire croître le taux de décomposition de l’éther (soit la vitesse de réaction) de plusieurs centaines de fois, sans que l’iode soit consommée. On montre que la vitesse de ce processus catalysé suit alors la règle suivante:

les crochets désignent la concentration du produit chimique indiqué, tandis que k est la constante cinétique du processus. Nous voyons que l’évolution de la concentration de l’éther fait intervenir le produit des concentrations de cette même substance et du catalyseur. Nous appelons fonction non linéaire ce type de dépendance. Les circuits électriques, l’optique, la mécanique des fluides, la géophysique et la biologie fournissent de nombreux autres exemples de non-linéarité.

D’une manière générale, soit x ¹, ..., x ⁿ un ensemble de variables décrivant le comportement d’un système macroscopique (concentrations chimiques, température, vitesse d’écoulement, etc.). Moyennant des hypothèses très générales, ces variables obéissent à des équations d’évolution de la forme: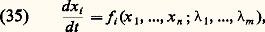

où¹, ...,^m représente une série de paramètres de contrôle intervenant dans les processus (constantes cinétiques, coefficients de transport, etc.), tandis que les fonctions f ⁱ décrivent la manière dont les variables s’influencent mutuellement. Une non-linéarité dans une de ces fonctions (par exemple, sous la forme donnée par l’équation 34) reflète l’existence des mécanismes de couplage entre des variables présentes dans le problème, en l’occurrence la concentration de l’iode et de l’éther.

L’objet de notre analyse est d’étudier le comportement des systèmes décrits par des lois non linéaires de la forme (35). Comme la non-linéarité ouvre la voie à des solutions multiples, on doit s’attendre à des transitions entre états, ainsi qu’à la coexistence de régimes qualitativement différents. Grâce à ces phénomènes, les systèmes non linéaires ont la capacité de présenter un comportement complexe qui se traduit souvent par des morphologies inattendues et fort diversifiées; c’est ainsi que la structure du flocon de neige ou celle de l’abdomen de la mouche drosophile , pour ne citer que deux exemples, sont des conséquences insoupçonnées d’une dynamique non linéaire sous-jacente.

Une première classification du comportement des systèmes non linéaires est fournie par la thermodynamique . L’objet de cette branche des sciences physiques est de dégager certaines propriétés caractérisant l’évolution des systèmes macroscopiques, qui soient largement indépendantes des détails des processus au niveau moléculaire. La plus importante de celles-ci est sans doute le second principe de la thermodynamique d’après lequel, dans un système isolé de son environnement, l’évolution conduit à un état où l’entropie, S, prend sa valeur maximale. C’est l’état d’équilibre thermodynamique ^{[cf. ENTROPIE]}. Un tel état est atteint également lorsque le système, au lieu d’être isolé, est maintenu à une température ou à une composition constantes (cf. THERMODYNAMIQUE - Lois fondamentales).

Revenons aux processus non linéaires. Un premier résultat établi par la thermodynamique est que, au voisinage de l’état d’équilibre, les non-linéarités ne peuvent jamais introduire un comportement nouveau (par rapport à celui qui caractérise l’équilibre lui-même), à une exception importante près: les phénomènes de transitions de phase. Dans ce cas, les différents modes du mouvement seront fortement couplés. En faisant varier certains paramètres d’état, telles la température ou la pression (notées par¹, ...,^m dans l’équation 35), on peut ainsi passer d’un état initial (disons la phase gazeuse) à une coexistence des phases (liquide-vapeur), ou enfin à une nouvelle phase (la phase liquide) différente de la phase initiale. Pour un tel comportement la première inégalité du critère de stabilité (30) n’est généralement plus satisfaite. Dans plusieurs cas (liquide-solide, para-ferromagnétique, etc.), ce passage s’accompagne d’une disposition régulière de certaines propriétés moléculaires ou atomiques dans l’espace: nous appelons ce phénomène un brisement de symétrie . Il en résulte un ordre spatial, que nous observons d’ailleurs très couramment dans la vie quotidienne en présence d’un cristal. Toutefois, cet ordre s’étend sur des distances microscopiques, de l’ordre du dixième de manomètre.

La situation est fort différente lorsqu’un système opère très loin de l’état d’équilibre thermodynamique. Comment réaliser un tel écart? Deux manières d’agir sur le système sont possibles. Ou bien on effectue délibérément une modification importante dans les conditions du fonctionnement en modifiant, par exemple, la température d’une de ses parties de plusieurs degrés: nous appelons cette action une perturbation . Le système va y répondre en évoluant vers l’équilibre, mais, durant cette évolution, il peut présenter un comportement inattendu pendant un intervalle de temps plus ou moins long. Ou bien on applique des contraintes permanentes sur le système. Par exemple, on peut maintenir deux parties de la surface limitrophe à des températures, pressions ou compositions fort différentes. Le système sera ainsi empêché d’atteindre l’équilibre aussi longtemps que les contraintes seront appliquées.

Depuis la fin des années soixante, il apparaît clairement que, dans les systèmes non linéaires, l’écart à l’équilibre peut donner lieu à des possibilités nouvelles de comportement complexe et de brisement de symétrie. En particulier, en franchissant un seuil critique d’écart à l’équilibre (cf. Critères d’évolution et de stabilité ), on peut observer à l’intérieur d’une seule phase de la matière des phénomènes spectaculaires connus sous le nom de structures dissipatives . Il s’agit de changements de régime conduisant à un ordre spatial, ou même à un ordre temporel, qui s’étend sur une échelle macroscopique de l’ordre des millimètres ou des minutes. On montre que le seuil critique de ces transitions est déterminé par une portion du taux de changement d’entropie du système qu’on appelle la production d’entropie d’excès, et qui reflète l’entropie produite dans le système par l’action des perturbations [critère de stabilité (30)].

Principales transitions dans les systèmes non linéaires hors d’équilibre

Examinons de plus près les propriétés qualitatives des solutions du système d’équations non linéaires (35), une fois que le seuil critique d’écart à l’équilibre a été franchi. Une étude détaillée montre que l’apparition d’un comportement complexe repose sur deux phénomènes d’une extrême généralité: l’échange de stabilité entre solutions, ainsi que la bifurcation de solutions multiples pour certaines valeurs caractéristiques des paramètres de contrôle que nous appellerons points de bifurcation.

Supposons que nous contrôlions de l’extérieur les valeurs d’un paramètre. Représentons une caractéristique quelconque des solutions des équations (amplitude, moyenne, module, etc.) en fonction de. Typiquement, pour inférieur à une valeur^c , le système a une seule solution (fig. 5). La thermodynamique nous enseigne que celle-ci est le prolongement de l’état d’équilibre, lorsque les contraintes éloignent progressivement le système de cet état: on l’appelle branche thermodynamique . En l’absence (supposée) de transitions de phase, on a donc, pour 麗^c , un comportement non ordonné caractérisé par une répartition uniforme des différentes propriétés du système dans l’espace et dans le temps. De plus, si on inflige délibérément une perturbation pour provoquer un éloignement de cet état, le système développe des mécanismes qui amortissent cette perturbation: nous appelons cette propriété la stabilité de la solution en question. La situation peut changer pour 閭^c . On observe alors la genèse de nouvelles solutions stables qui coïncident avec la première pour =^c , mais qui bifurquent au-delà de celle-ci, devenue instable, pour 礪^c : nous appelons ce phénomène la première bifurcation .

Examinons le comportement qui accompagne l’apparition de ces solutions multiples, dans un premier cas. Lorsque le paramètre varie de façon continue, le changement d’une certaine propriété (la concentration d’une substance chimique, la température, etc.) survient de façon discontinue, sous forme d’un saut. De plus, un accroissement des valeurs de ce paramètre, suivi d’une décroissance, conduit le système à des branches de solution différentes: nous appelons ce phénomène comportement en hystérésis (fig. 6). Il s’agit d’un phénomène extrêmement répandu dans la nature, qui reflète un changement des propriétés fonctionnelles du système. Il est observé dans les substances magnétiques, les membranes artificielles ou biologiques, ou enfin dans les écoulements fluides.

Un second phénomène peut arriver au-delà de la première bifurcation. Au lieu d’évoluer vers un état permanent, les variables du système exécutent des oscillations entretenues parfaitement reproductibles, dont les propriétés (amplitude, période, etc.) ne dépendent que des caractéristiques internes du système (fig. 7). On observe que le même mouvement est accessible en partant initialement d’états fort différents.

Cette propriété reflète la stabilité du comportement périodique, que nous appelons un cycle limite . Avec la bifurcation de ce mouvement, le système «découvre» la notion du temps et la notion de la phase, tandis qu’avant la bifurcation ce même système ne peut pas percevoir ces notions puisqu’il s’établit toujours sur un régime stationnaire. Nous disons que le cycle limite brise les symétries temporelles. L’intérêt considérable des cycles limites est qu’ils constituent le prototype des rythmes endogènes pouvant prendre naissance dans les systèmes physico-chimiques tels, notamment, les rythmes biologiques à l’échelle métabolique, épigénétique ou circadienne.

Donnons un dernier exemple de comportement associé à la première bifurcation. Cette fois, les variables du système tendent vers un état permanent, mais, ce faisant, elles donnent naissance à une différenciation spatiale: l’espace qui abrite le système est subdivisé, spontanément, en compartiments caractérisés par des valeurs différentes de ces variables. Avec cette bifurcation, le système «découvre» donc la notion de l’espace qui est totalement absente de l’état uniforme antérieur à la bifurcation. Ce brisement des symétries spatiales peut être accompagné par la genèse d’un axe d’orientation privilégié (fig. 8), permettant au système de distinguer le côté «gauche» du côté «droit», le «haut» du «bas».

Ainsi donc, loin de l’équilibre, les systèmes non linéaires peuvent présenter de façon spontanée un comportement complexe. Jusqu’où peut conduire cette auto-organisation ? Que se passe-t-il au-delà de la première bifurcation? La réponse à ces questions commence seulement à être connue. Elle repose sur la notion des bifurcations en cascade , produites lorsque l’on contrôle simultanément un grand nombre de paramètres du système (cf. équation 35). Ce mécanisme donne lieu à une énorme variété des morphologies, caractérisées par des brisements successifs de symétrie conduisant à des asymétries spatiales très prononcées, par des comportements spatio-temporels inattendus sous forme d’ondes de propagation, ou enfin par l’apparition de comportement chaotique dans l’espace ou dans le temps.

Origine microscopique des bifurcations

La brève discussion du phénomène de bifurcation qui a précédé montre que pour certaines valeurs particulières des paramètres de contrôle (ou contraintes), un système non linéaire peut se trouver devant un choix critique : le chemin qu’il suivait (fig. 5, la branche a) n’est plus accessible. Il doit dès lors passer sur une branche (b) ou (b ) pour prendre le cas le plus simple d’un choix binaire.

En réalité, ce choix n’a rien d’un phénomène régulier. Il est caractérisé par l’apparition de cassures, de catastrophes, traduisant le conflit qui naît devant la dégénérescence du choix: (b) ou (b ). Le système tâte le terrain, amorce quelques faux départs, revient sur sa position initiale. Finalement, après ces hésitations, la dégénérescence est levée et une branche particulière est choisie (disons b), qui est suivie pendant tout un temps. Remarquons que, selon la branche choisie (par exemple b au lieu de b), le système subit une évolution tout à fait différente. Nous voyons donc apparaître un élément historique associé étroitement à la notion de bifurcation et de choix critique.

Dans un système macroscopique, comportant plusieurs sous-unités en interaction, il existe un mécanisme naturel permettant d’explorer les différentes possibilités qui lui sont offertes au moment du choix critique: ce sont les fluctuations statistiques . En effet, l’observation de l’état d’un système fait apparaître des moyennes des valeurs instantanées des différentes variables d’état, soit sur le temps, soit sur le volume de la mesure, qui sont tous les deux de dimensions macroscopiques. Dans chaque petit élément du système, il se produit alors continuellement des écarts à la moyenne: ce sont les fluctuations. On montre que les lois d’interaction des différents éléments d’un système physico-chimique sont telles que ces fluctuations présentent un caractère aléatoire. Aussi, la manière la plus naturelle de les décrire consiste-t-elle à introduire une distribution de probabilité P( 﨡¹, ..., 﨡ⁿ ; t ) décrivant les chances qu’on a d’observer, à l’instant t , les écarts 﨡¹, ..., 﨡ⁿ autour des valeurs x ¹, ..., x ⁿ qui, elles, obéissent aux lois d’évolution macroscopiques données par l’équation (35). Moyennant des conditions très générales, on montre que cette distribution obéit à une équation connue sous le nom d’équation maîtresse :

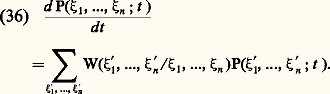La grandeur W représente la probabilité de transition par unité de temps entre un état ( 﨡 ¹, ..., 﨡 ⁿ ) et l’état ( 﨡¹, ..., 﨡ⁿ ); sa structure reflète les non-linéarités des lois d’évolution dynamiques (cf. équation 35), bien que l’équation (4), elle, garde une structure linéaire.

L’étude de l’équation (36) montre qu’au voisinage des points de bifurcation les fluctuations présentent un comportement anormal, traduit par un couplage extrêmement fort entre les différentes parties du système. Dans certaines conditions, ce couplage est tellement contraignant qu’il conduit à la suppression pure et simple de la bifurcation. C’est ainsi que des systèmes à une dimension spatiale ne parviennent jamais à franchir le seuil de bifurcation, à cause des fluctuations. Au-delà d’une seule dimension, la bifurcation peut avoir lieu. Toutefois, elle est alors accompagnée des divergences de certaines propriétés des fluctuations, ainsi que de l’apparition des corrélations à longue portée envahissant les différentes parties du système qui agissent de manière concertée: nous appelons ce comportement, qui est le prélude de l’ordre macroscopique apparaissant au-delà de la bifurcation, l’ordre par fluctuation .

Exemples

Donnons un bref aperçu des systèmes capables de présenter un comportement complexe, grâce au mécanisme de bifurcation loin de l’équilibre thermodynamique.

Systèmes biologiques

Les systèmes vivants ont des capacités très prononcées de stocker de l’information et d’adapter leur comportement en fonction des stimuli reçus de l’environnement. Cette adaptation est essentielle pour le développement et la survie d’un organisme. Parmi ses manifestations les plus frappantes, on compte les rythmes innés de périodes diverses, ainsi que la genèse de formes spatiales lors du développement embryonnaire des organismes pluricellulaires. La modélisation mathématique de ces processus fait l’objet d’une discipline en plein développement, la biologie théorique . On y montre qu’un grand nombre de manifestations de l’ordre biologique sont associées à des bifurcations permettant au système de présenter plusieurs solutions (cf. supra : Thermodynamique et biologie ).

Optique quantique

Soit une population d’atomes plongés dans un champ électromagnétique. Si le champ extérieur est faible, les atomes émettent du rayonnement en se désexcitant de manière aléatoire. Par contre, si le champ extérieur dépasse un seuil, les interactions entre dipoles atomiques font que les atomes émettent en phase: c’est le phénomène d’émission cohérente par laser . Soit E, la valeur instantanée (qui est un nombre complexe) du champ électrique de la lumière du laser; on montre que, E obéit à une équation de la forme (35):

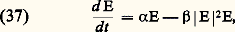pour un laser à un seul mode, où 見 est le «gain non saturé» et 廓 la «constante de saturation». On démontre que le seuil d’émission de lumière cohérente se traduit par une bifurcation donnant naissance à des solutions stationnaires multiples de l’équation (37).

Circuits électriques

Plusieurs circuits comportant des éléments, tels que les tubes électroniques, les transformateurs, etc., induisent des dépendances courant-tension d’une forme non linéaire. Un exemple frappant est le circuit de Van der Pol (couplage inductif d’une triode et d’un circuit résonnant) décrit par l’équation:

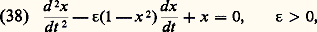où x est lié à la tension aux bornes de l’inductance et 﨎 dépend des différents paramètres du circuit. Cette équation a bien la forme (35) si on pose dx /dt = y . On montre qu’elle admet une bifurcation menant à un cycle limite. Ce phénomène est connu en électronique sous le nom d’auto-excitation .

Réactions chimiques

Les systèmes de la cinétique chimique sont de la forme (35), où les fonctions f ⁱ représentent les taux de production ou de consommation du constituant i . Il existe plusieurs exemples d’oscillateurs chimiques et biochimiques présentant des bifurcations qui font apparaître des cycles limites: système glycolytique, réaction de Belousov-Zhabotinski (cf. photo), entre autres.

Mécanique des fluides

Les écoulements des fluides soumis à des contraintes thermiques, ou mécaniques, donnent de nombreux exemples de bifurcation des trois types (décrits par les figures 6, 7 et 8). Un exemple frappant est l’amorce des mouvements organisés dans l’espace sous forme cellulaire, dans une couche horizontale d’un fluide chauffée par en dessous (instabilité de Bénard). Ces mouvements ont une importance considérable en géophysique et en astrophysique (circulation atmosphérique générale, tectonique des plaques, origine du champ magnétique planétaire). À la limite où les contraintes thermiques deviennent très importantes, on passe souvent à des mouvements chaotiques associés à des bifurcations en cascade. Ces transitions marquent aussi le début du phénomène appelé Turbulence. Des contributions récentes consacrées à ce sujet ont permis de mieux comprendre les mécanismes fondamentaux de ce phénomène encore incomplètement éclairci.

Encyclopédie Universelle. 2012.